ExcelでCHISQ.TEST関数を利用して、カイ二乗(χ2)検定をする手順を紹介します。
書式は以下の通りです。
CHISQ.TEST([実測値の配列・セルの範囲], [期待値のの配列・セルの範囲])
おみくじの箱にくじが5つ入っています。4つがはずれで、1つがあたりです。6人がくじをそれぞれ一人5回引き、当たった回数、はずれた回数を記録します。結果は以下となりました。
| 名前 | あたり | はずれ |
|---|---|---|
| ぺんた | 0 | 5 |
| あでりー | 2 | 3 |
| ろっくほっぱー | 1 | 4 |
| きんぐ | 3 | 2 |
| えんぺらー | 0 | 5 |
| ぐれい | 1 | 4 |
このとき、人によってくじのあたり方に差があるでしょうか(エスパーみたいな人がいる、または、くじ箱に細工がしてあるなど)
くじは公平で誤差の範囲内でしょうか?
帰無仮説は差がない、誤差のない仮説となるため「人によってくじのあたり方に差はない」となります。
最初に下図の表を作成します。期待値通りに全員にあたりが出たとします。
| 名前 | あたり | はずれ | あたり期待値 | はずれ期待値 |
|---|---|---|---|---|
| ぺんた | 1 | 4 | 1 | 4 |
| あでりー | 1 | 4 | 1 | 4 |
| ろっくほっぱー | 1 | 4 | 1 | 4 |
| きんぐ | 1 | 4 | 1 | 4 |
| えんぺらー | 1 | 4 | 1 | 4 |
| ぐれい | 1 | 4 | 1 | 4 |
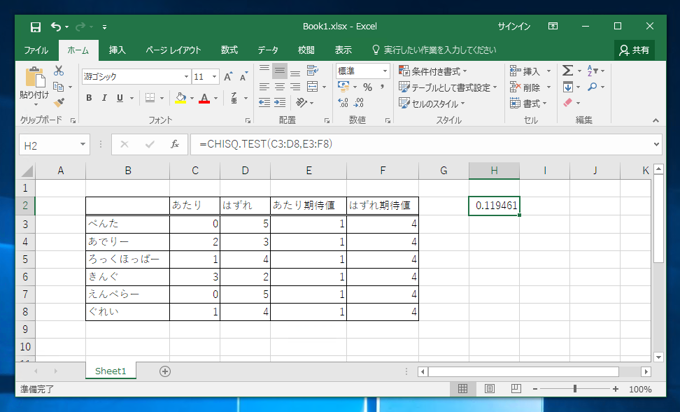
H2セルに下記の数式を入力します。
数式を確定すると、H2セルには、"1" が表示されます。期待値と観測値が全く同じため、適合度は100%となります。
続いて、条件をふまえた下図の表を作成します。
| 名前 | あたり | はずれ | あたり期待値 | はずれ期待値 |
|---|---|---|---|---|
| ぺんた | 0 | 5 | 1 | 4 |
| あでりー | 2 | 3 | 1 | 4 |
| ろっくほっぱー | 1 | 4 | 1 | 4 |
| きんぐ | 3 | 2 | 1 | 4 |
| えんぺらー | 0 | 5 | 1 | 4 |
| ぐれい | 1 | 4 | 1 | 4 |
| 名前 | あたり | はずれ | あたり期待値 | はずれ期待値 |
|---|---|---|---|---|
| ぺんた | 3 | 17 | 4 | 16 |
| あでりー | 2 | 18 | 4 | 16 |
| ろっくほっぱー | 1 | 19 | 4 | 16 |
| きんぐ | 5 | 15 | 4 | 16 |
| えんぺらー | 4 | 16 | 4 | 16 |
| ぐれい | 6 | 14 | 4 | 16 |
この場合、H2セルの値は、"0.312..."となり、5回の時よりも適合度が高くなり仮説は棄却できず、人による出方の違いは無いことが言えます。
ここで、「ろっくほっぱー」があたりが16回出たとします。(はずれは4回)
この状態でH2セルの値は、"0.00000000033"となります。有意水準を5%すすると、0.05より低い値のため、、「人によってくじのあたり方に差はない」の仮説は棄却され、人によって当たりはずれに差があることが言えます。

